凸関数と非凸関数
凸関数の定義と例
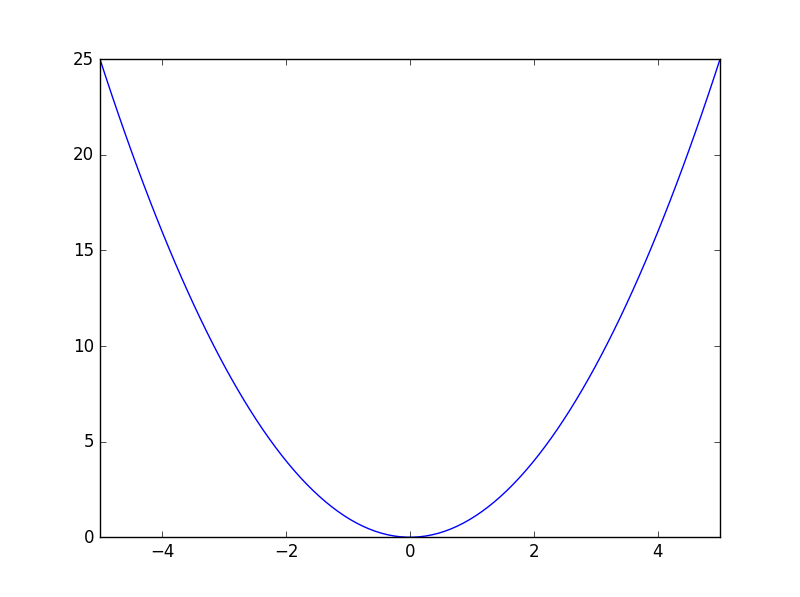
凸関数の最たる例は、二次関数$f(x)=x^2$です。
凸関数の正確な定義は以下の数式で表されます。 \[ \forall x_1, x_2 \in X, \forall \in [0, 1]: f(tx_1+(1-t)x_2) \leq tf(x_1)+(1-t)f(x_2) \] ちょっと記号が多く、むずかしい数式のように見えます。 しかしこれは、あるひとつの単純な公式で解き明かすことができます。
不等式の右辺に着目してみましょう。t, (1-t)という文字が見えますね。 これはベクトルの内分点の公式です。 つまり右辺は、点$(x_1, f(x_1))$と点$(x_2, f(x_2))$の内分点を表しているのです。
そして不等式の左辺は、関数fの引数に、内分点の式がそのまま入っています。 つまり、$x_1 \leq x \leq x_2$の範囲の$f(x)$を指しています。
これらを不等号で結ぶと、次のように言い換えられます。 「関数$f(x)$のある二点間の値が、その二点を結ぶ直線よりも常に小さい」と。
ためしに$y=x^2$などで試してください。 どこの2点を選んで直線を引いてみても、関数$f(x)$のカーブが下に来ているはずです。 この性質を、凸性と言います。
非凸関数
凸関数でなければ、非凸関数です。 三次以上の関数は、往々にしてこの非凸関数です。
凸関数と非凸関数の例を、直線を引いてあるものを
ローカルミニマムの罠
非凸関数は最小値の他に極小値(ローカルミニマム)を持ちます。 極小値とは関数の「谷」にあたる部分であり、 他にもっと深い「谷」があるときに、そこを極小値と言います。 一番深い「谷」は最小値と呼ばれます。
何の対策もせずに勾配法を実行していると、 このローカルミニマムにすっぽりとはまり込んでしまうことがあります。
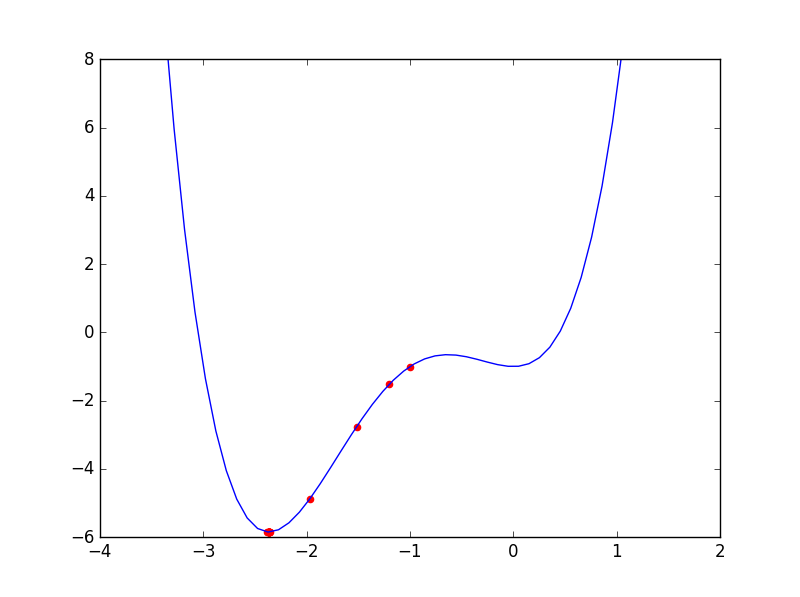
はまり込むとは、どういうことでしょうか。 まずは関数$f(x)=x^4+4*x^3+4*x^2-1$に、初期値$x^{(0)}=-0.5$で勾配法を実行する流れを見ていきましょう。
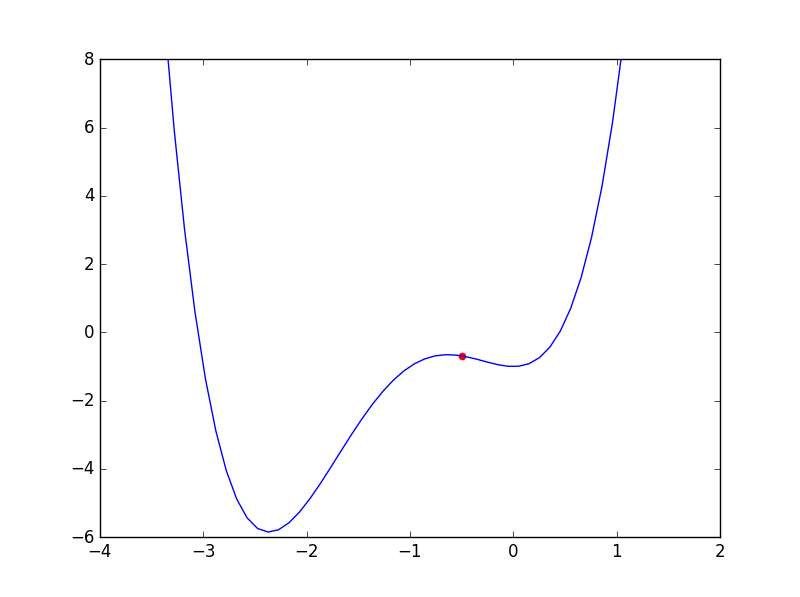
上の図の赤い点が、最小値候補の初期値です。
これに対して勾配法をしばらく実行してみましょう。
累計で20回更新すると、以下のような候補値になります。
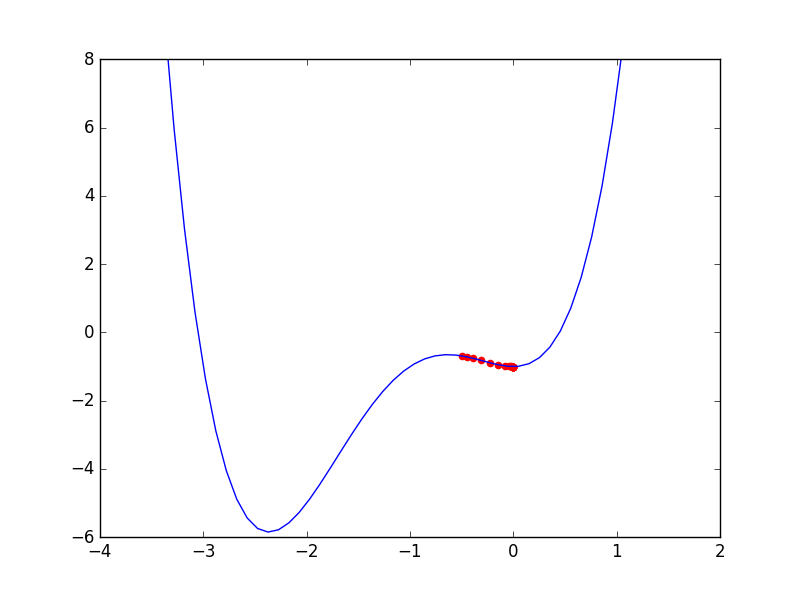
20回更新したところ、最小値候補は$x=0.0000...$という値になりました。
あれれ?おかしいですね。 グラフを見る限り、最小値は-2と-3の間にあるはずなのですが、 0の付近で最小値候補の更新が止まってしまいました。
これこそがローカルミニマムにはまり込む、という現象です。 勾配法は導関数に応じて値を更新するのですが、 極小値(ローカルミニマム)も、最小値も、ひとしく導関数が0になるのです。
無策の勾配法ではこの見分けがつかないため、 一度ローカルミニマムに陥ってしまったら、もう最小値を探すことはできなくなります。